Dialogue on venous hemodynamics
Fedor LURIE,2 MD, PhD;
Giorgio BERGAMO,3 BSc;
Sara GUERZONI,4 BSc;
Marzia LUGLI,1 MD
1Vascular Surgery, Hesperia Hospital,
Modena, Italy
2Jobst Vascular Institute and the Division of
Vascular Surgery at the University of
Michigan, Ann Arbor, Michigan, USA
3Microlab Elettronica Sas. Padova, Italy
4Fleboxan Vein Clinic, Modena, Italy
Abstract
Hemodynamics of the venous system of the lower limbs is very complex, its explanation typically evoking formulas and concepts that can be daunting for those new to the subject. Here, we approach the task from a more conversational angle, introducing a dialogue between expert and student as they discuss the matter. Such an approach aims to encourage further interest and pursuit of deeper understandings.
Introduction
The hemodynamics of the venous system of the lower limbs is very complex. The explanation of physiology and pathophysiology takes place through the application of mathematical formulas and physical concepts not always well understood by young phlebologists who approach the subject. The result is that you discourage them from studying instead of encouraging them. This dialogue between the teacher (Prof Smith)–a senior phlebologist–and his student (Dr Paul) tries to explain in a very simple way and without using any formula the most elementary concepts that characterize the venous system of the lower limbs. We hope to arouse interest and push young phlebologists to deepen this fascinating and still in some ways obscure field of physiopathology.
Take-home message
The premise for improving each therapeutic gesture is to try to understand how it acts and which pathophysiological element it modifies. Understanding some basic elements of the lower-limb venous system improves our daily decisions about phlebological actions.
Dialogue
Dr Paul: Today my legs feel a bit heavy. Maybe I have venous hypertension.
Prof Smith: In that case you can relax. What we normally call “venous hypertension” doesn’t exist.
Dr Paul: What do you mean “it doesn’t exist”?
Prof Smith: I’m joking, but only in part. It’s a long way to the Convention. If you like, we can spend the journey talking about some basic principles in venous pathophysiology.
Dr Paul: Sure. It would be a pleasure.
Prof Smith: Excuse me for asking. I assume you know the basic difference between arteries and veins?
Dr Paul: I think so.
Prof Smith: Ok, but let me give you a briefing. The venous system is quite different from the arterial system.1,2 As you know, in the arterial system we find high pressure, low volumes, noncollapsible arterial vessels, and high peripheral resistance in the limbs. Whereas in the venous system, we see lower pressure, higher volumes, collapsible venous vessels, with low peripheral resistance.
Dr Paul: Low pressure? How come low pressure? I thought that in a subject of average height, venous pressure at the ankle exceeded 100 mm Hg.3
Prof Smith: Of course. I see what you mean. Let’s backtrack a bit. Being on planet Earth, we are subject to the law of gravity. This means that when we stand still, a column of blood of a certain weight forms in the venous system.
Dr Paul: I see … and increasing the vein caliber, I suppose we increase the weight.
Prof Smith: Wrong! The weight in question depends on a person’s height. The vein diameter has nothing to do with it.4 You remember Torricelli!
Dr Paul: Vaguely …
Prof Smith: Torricelli took a series of wine-butts like the ones you use at home to make “aceto balsamico.” He filled them with water and connected tubes at various heights and with various diameters. He also filled the tubes with water.
Dr Paul: Then what happened?
Prof Smith: When the column of water reached a certain height, the wine-butt broke. The amazing thing was that the wine-butt broke regardless of the tube’s diameter – narrow or wide (Figure 1).
Dr Paul: You mean the liquid exerts pressure proportional to its height, and the diameter is not a key factor.
Prof Smith: Exactly! You got it!
Dr Paul: So, what you’re saying is that an incontinent, great saphenous vein of wide caliber has the same pressure as an incontinent great saphenous vein of small caliber, in subjects of the same height.
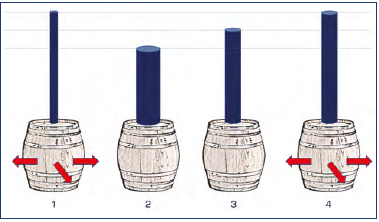
Figure 1. Torricelli’s law. The pipes above the barrels are filled with liquid. The pressure exerted will break first barrels, number 1 and 4 (of equal height), regardless of the caliber of the tube.
Prof Smith: Exactly! Those veins have the same hydrostatic pressure.
Dr Paul: But a patient with a wide varicose vein usually is more symptomatic than a patient with a narrow vein.
Prof Smith: That’s right. But to explain the difference we don’t look at the pressure.
Dr Paul: What do we look at?
Prof Smith: Other parameters. But let me first finish what I was saying about venous pressure.
Dr Paul: I’m all ears. You were talking about pressure, so that means hydrostatic pressure. Is that right?
Prof Smith: That’s right. We ought really to call it “hemostatic pressure” because we are talking about a column of blood, and not water. Even if the term “hydrostatics” is usually used.
Dr Paul: I’m with you. This pressure is the force that makes the blood return to the heart, right?
Prof Smith: Wrong again! It’s not this pressure that moves the blood. Let me give you an example to make things clear. If I take a cylinder 1 meter in height and fill it with water, the hydrostatic pressure at the bottom of the cylinder is 73 mm Hg. Although the pressure at the bottom is higher than it is at the surface, the liquid doesn’t move.
Dr Paul: Why not?
Prof Smith: Because at the surface the liquid has a potential energy equal to that at a height of 1 meter. So, the 2 forces are equal and opposite. Otherwise, we’d have discovered perpetual motion!
Dr Paul: Let me see if I understand. At ground level, the hydrostatic pressure is high, and the potential energy is zero. And vice versa at a height of 1 meter.
Prof Smith: Exactly.
Dr Paul: And at half-way up?
Prof Smith: At half-way up, the 2 energies are perfectly equal (Figure 2).
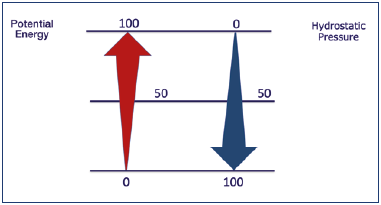
Figure 2. Hydrostatic pressure and potential energy. Where the hydrostatic pressure is maximum, the potential energy is minimum and vice versa.
Dr Paul: I get it. But I don’t quite understand the concept of potential energy.
Prof Smith: Potential energy can also be called gravitational energy. Think about the water level in a dam serving a hydroelectric power plant. The potential energy is the difference in height between the height of the water in the dam and the base of the dam itself.
Dr Paul: So, in that case, it isn’t the difference in pressure that moves the blood.
Prof Smith: You’ve got it! It isn’t the pressure gradient but the energy gradient.
Dr Paul: But who or what supplies this energy?
Prof Smith: When a patient is standing still, the energy comes from cardiac contraction.
Dr Paul: I know that. But if I remember correctly, this energy is dissipated at the capillary level.
Prof Smith: So how do you think the blood returns from the foot to the heart?
Dr Paul: Respiration, cardiac aspiration, the artery pulsing next to the vein, muscle contraction, and so on.
Prof Smith: Wrong. The blood also returns when you hold your breath and when there are no muscular contractions. What makes the blood return to the heart is a principle known as vis a tergo, which is provided by the heart.
Dr Paul: Give me another example, please.
Prof Smith: Think of an elevator. Do you know how an elevator works?
Dr Paul: More or less.
Prof Smith: Maybe it’s more helpful if you think of a U-shaped tube, with its two branches filled with a liquid. The level of the liquid will be equal in both branches. You only have to blow lightly into one end to see the liquid overflowing at the other end. That’s not the whole story, because you don’t find a system of rigid tubes in nature. Still, the analogy is valid for the time being (Figure 3a).
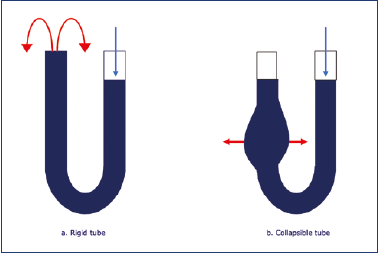
Figure 3. a) In a rigid tube containing liquid, the pressure exerted on one end produces a displacement of the liquid toward the other end. b) In a partially collapsible tube, the transmitted energy initially expands the tube itself.
Dr Paul: But if the pressure in the vein is due exclusively to the distance from the heart, when is it correct to talk of venous hypertension?
Prof Smith: Apart from particular pathologies, such as vein occlusion (mainly acute) and vein malformations, venous hypertension, as such, in the standing (orthostatic) position… does not exist.
Dr Paul: But what about hypertension in de-ambulation? I mean when a patient is walking and has damaged or absent valves? You remember the graphs that are presented at every convention? What’s happening there?
Prof Smith: Right. I’ll show you that photo. I have it in my phone. Here we are. This is not a case of venous hypertension. Rather, it is the absence of a reduction in venous pressure. It is not that the pressure goes up, but simply that it fails to go down.5,6
Dr Paul: Let’s have a cup of coffee while I have a good think about all this …
Prof Smith: In healthy subjects with valves, hydrostatic pressure in the veins decreases while they walk (Figure 4). This is because continent valves break up the column of blood we mentioned earlier.
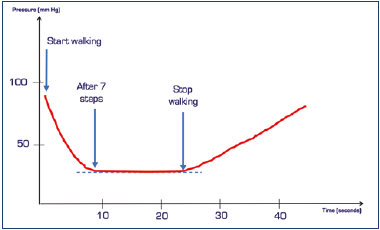
Figure 4. Venous pressure, detected with a needle placed in a dorsal vein of the foot, during walking.
Dr Paul: In other words?
Prof Smith: In other words, when the valve closes at femoral level, the column of blood in question will be the one that goes from that point (ie, the femoral valve) to the foot, and not the one that goes from the right atrium to the foot. Practically half the length. If a valve then closes at a lower point, say at popliteal level, the length is further reduced, and so on until a minimum, which is around 25-30 mm Hg.
But we’re oversimplifying. It doesn’t happen simultaneously this way in all the veins in a limb.7 The column of blood doesn’t divide if there are no continent valves (Figure 5).
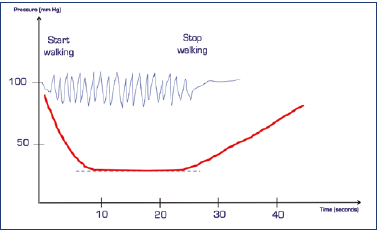
Figure 5. When the valves do not work, venous pressure is not reduced during walking. This represents the absence of physiological hypotension.
In such cases, we always used to talk about “venous hypertension.” As you can now see, it was actually a decrease in pressure that failed to take place.8
Remember that in the orthostatic position, hydrostatic pressure accounts for 80% of venous pressure. That’s why it’s so important. To get an idea of what happens, we can take a plastic bottle and make holes in it at various levels. What we observe is that the lowest hole produces a jet of water that goes further than the others (Figure 6).
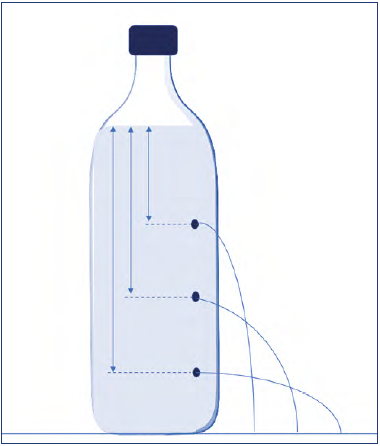
Figure 6. The lowest point has a higher hydrostatic pressure. By making a hole at this level, there will be a longer jet of water.
Dr Paul: But I thought you said that the system is immobile.
Prof Smith: That’s right, I did. But if you make holes in the system, the situation changes from a static to a dynamic one. If we inject liquid to keep the level constant, the lowest hole has a longer jet, and the highest hole has a shorter one.
This shows that pressure-derived energy is being transformed into kinetic energy.
Dr Paul: Got it. Apart from hydrostatic pressure, what other factors are involved in venous pressure?
Prof Smith: Static pressure directed toward the vein walls, and dynamic pressure, derived from the vis a tergo; but other factors are involved.
During muscle contraction, when intramuscular veins are squeezed, an increase in velocity is created, which can modify the energy. This is because the sum of the various energies is constant, in line with Bernoulli’s law.
Dr Paul: I’m not quite with you.
Prof Smith: Remember that the three kinds of energy– hydrostatic, static, and dynamic–act in combination. As one kind increases, the others diminish in quantity. Incidentally, dynamic energy is more correctly defined as “kinetic energy” and is correlated to the speed of flow. However, blood volume is also a key factor. Now, we need to talk about vein anatomy.
Dr Paul: I’m still listening.
Prof Smith: Veins are collapsible tubes.
Dr Paul: Right.
Prof Smith: Collapsible tubes vary in diameter according to the amount of liquid they contain. Imagine a plastic bag filled with water and then empty.9 The venous system is a kind of expanding reservoir that can change its capacity to cope with the amount of blood it needs to contain.10
Dr Paul: You mean compliance?
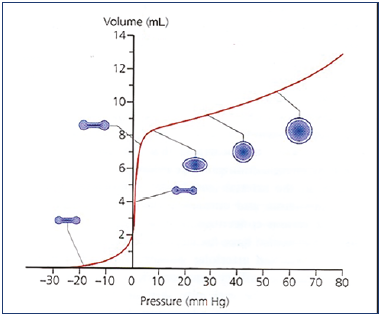
Prof Smith: Exactly. This ability to vary its capacity is called compliance. Compliance is one of the key factors in the venous system. When empty, a vein presents a flattened profile. When it fills, it takes on a spherical shape in transversal section. When particularly full, it can widen to a point of maximum expansion. This depends on vein-wall pliability.
When the vein begins to fill, it maintains a very low pressure until a spherical shape is achieved. From then on, the pressure will increase, and even small variations in volume will be enough to create high increases in pressure (Figure 7).
Volume and pressure also vary depending on the anatomical location of the vein and on the position of the body. Take the lower cava system, for example.
Dr Paul: So, the legs.
Prof Smith: Exactly. In the lying position, in certain locations, the leg veins can collapse, whereas in the standing position they fill up. The venous system will accumulate energy by means of wall distension. Before reaching this energy, the blood in the large veins is practically motionless. If you want proof of this, take a duplex probe and place it on the femoral vein in a lying subject. Now have the subject stand up and you will see that there will be a certain amount of time before you can hear a signal. This is due to the filling time of the system and the accumulation of parietal energy.
The analogy of the U-shaped tube I mentioned before is slightly misleading. In veins, one of the branches of the U has a collapsible tube (Figure 3). So, before it transfers its energy, it needs to acquire parietal pressure and distend to its maximum. Also, each vein has a different degree of compliance.
Dr Paul: When you speak about collapsible tubes, what happens in the superior cava system?
Prof Smith: Thank you for the question because jugular veins offer a good example of what we mean when talking about collapsible veins.
Let me first say that each system has its own particular characteristics. So, we can’t extend these principles to all the veins in the body. However, to give you a better idea of what we mean when we talk about collapsible veins, I want to use the example of the jugular veins.
Dr Paul: Please do.
Prof Smith: When a patient suddenly stands up from supine position, blood will flow rapidly toward the heart, whereas blood from the arterial system can’t fill the vein fast enough to maintain the volume at what it was when the patient was lying down. So, the vein caliber has to adapt to a lower volume of blood. In other words, the container adapts to the contents. And when this happens, the various resistances adjust to each other.
Let me give you a more graphic example. Imagine you have a bathroom sink full of water. Now remove the plug, leaving the tap running. Once the sink has emptied, the only flow of water going down the plughole will be what is coming out of the tap. All you see is the water going down the plughole. But in the part of the sink where there is no water, there is air! In veins there is no air, and that is why the vein has to adapt to the contents.
In a collapsible tube (ie, the vein), the wall has to distend to accumulate the energy required.
During muscle contraction, when intramuscular veins are squeezed, an increase in velocity is created, which can modify the energy. This is because the sum of the various energies is constant, in line with Bernoulli’s law.
Dr Paul: What other factors accelerate blood flow?
Prof Smith: Another factor is anatomic. Throughout the system, the global vein section narrows from foot to heart. This is what explains the increase in velocity. The leg often has a double system, but we have a single common femoral vein. Remember that the amount of blood flowing through the common femoral artery is equal, per unit of time, to that flowing through the common femoral vein. That is when other smaller pathways are excluded.
Dr Paul: Is this always the case?
Prof Smith: No, this situation changes continuously according to the collapsible vein concept. Take the example of a sprinter. As he or she runs, three things increase: cardiac output, arterial flow to the legs, and venous return. But after a few seconds, peripheral vasodilation occurs. This leads to a decrease in peripheral arterial resistance, and an increase in arterial flow. It’s Poiseuille’s Law. The volume of blood circulating redistributes to benefit the legs. Increased flow in the veins reduces lateral pressure, which minimizes venous dilation. When the sprinter stops running, cardiac output goes down rapidly. The venous flow slows down, and the lateral pressure increases, so the vein dilates, accumulating a lot of extra blood volume. As this happens, the flow through the common femoral artery becomes greater than that flowing through the common femoral vein. This is a good example of the way the venous system adapts. The high compliance of the venous wall means that the veins act as a buffer between the arterial flow to the leg and the venous return needed to maintain cardiac output at the right level.
Dr Paul: Are there other factors that increase velocity?
Prof Smith: Yes, valves. In the healthy subject, the valve not only prevents reflux, but also accelerates flow.
Dr Paul: How does this work?
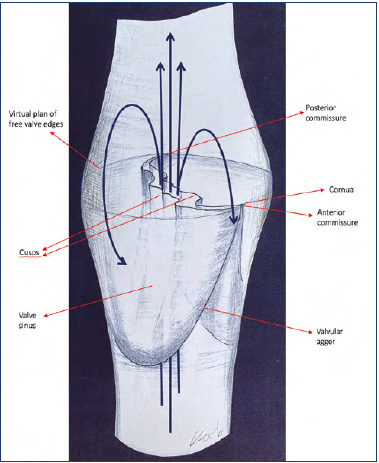
Prof Smith: It’s due to the position of the valve cusps, which maintain a semi-open state (Figure 9).
Dr Paul: But if they are in a semi-open state, don’t they also create higher resistance?
Prof Smith: Yes. In certain situations, a valve that doesn’t open correctly can be an obstacle to flow. This results in higher resistance.
Dr Paul: And when it opens correctly?
Prof Smith: When blood flows through a valve of a standing patient, we normally see only the central portion of the flow; this is not a smooth flow, but a turbulent one. When the muscle contracts, the valve leaflets open, but never fully. Valve resistance is therefore a flow-control mechanism to cope with changed needs.11,12
Actually, each of the valves works as a resistor in the venous system. However, there are several mechanisms that compensate for the increased resistance. The valve orifice has a “fish mouth” shape. When the shape shifts from the cylindrical to the fish-mouth shape (that of the valve funnel), a rotational momentum occurs in the blood moving through the vein. As the venous flow increases, it becomes helical (or spiral). This flow pattern is maintained due to a mechanism whereby each valve in a pair of valves orients at an angle to its partner. Finally, all venous tributaries join the vein at an angle, reinforcing the spiral flow pattern. Spiral flow is much more energy-efficient, which compensates for increased resistance in the valves.13
Dr Paul: We talked about resistance, and this reminds me of something. I heard in the last conference that obstruction through increased resistance is also important in determining the signs and symptoms of chronic venous disease.
Prof Smith: That’s right, reflux alone has long been valued; however, both obstruction and reflux are important. In a system of collapsible vessels, resistance plays a fundamental role, and given that in PTS they are associated with reflux in two-thirds of cases, you can understand its importance.14,15
Resistance is an obstacle to blood flow. The main obstacles are reduced diameter and length of the vein. Resistance is proportional to 8 times the length and inversely proportional to the vein radius to the fourth power.
Acute vein occlusion creates the highest resistance.
During an acute obstruction, the pressure is immediately distal to obstruction, similar to what you see during surgical clamping. Then a collateral pathway forms or dilation takes place, and the pressure drops. When you remove the clamp, the system empties, and the veins return to their usual size. They don’t follow the filling and emptying mechanism. At first, emptying is instantaneous, and then it gradually drops off.
A non-ideal elastic system, when distended, does not follow the same process of an ideal material.
Dr Paul: That is?
Prof Smith: When you apply a force and you obtain a linear elongation of the material, this is defined as “ideal.” A blood vessel is a viscoelastic tissue. If you apply a force, it changes shape. When the force decreases, the elastic tissue returns to its previous shape. But by reducing the force, we don’t get a reverse version of the widening process.
Dr Paul: Could you give me a clear example of pressure/ volume correlation in acute phase?
Prof Smith: The clearest proof of the way volume and pressure are related comes from occlusion plethysmography. When you inflate the pressure sleeve to 80 mm Hg, at a certain point you see a plateau.16,17
Dr Paul: What does this plateau mean?
Prof Smith: It means the blood is flowing in the veins again. The sleeve has simply created a dam effect.
Dr Paul: And what happens if we increase the pressure to 100 mm Hg?
Prof Smith: We get another plateau. It means the blood is flowing in the veins again. The sleeve has simply created a dam effect.
Dr Paul: But can’t the veins get blocked?
Prof Smith: Sure, but the values remain close to those of arterial pressure. Yes, like those you see during a total blockage, as in surgical clamping. Then what happens is a collateral pathway forms or dilation takes place and the pressure drops. In the chronic phase, the occlusion will be compensated by collateral pathways and a decrease in resistance.
Dr Paul: I’ve seen several phlebograms showing compensating collateral pathways.
Prof Smith: Yes, but pay attention, because when we look at a compensation circle during an investigation like phlebography, we are inclined to think that the system is compensated. This is not always the case. To compensate an occluded iliac vein with a diameter of 16 mm (that is, to equalize the flow with the same pressure and length) 256 veins are required with a calibre of 4 mm. So, a radiological image of a collateral pathway does not mean that the flow is normal.
Dr Paul: We spoke about resistance, but what happened with venous pressure?
Prof Smith: An increase in pressure gradient. In all events, during the chronic phase in basic conditions, you can’t increase the pressure distally, but during movement, things are different. In this case, pressure may increase, even if only slightly when collateral pathway is not efficient.
Dr Paul: What happens if these collateral pathways can’t compensate the obstruction?
Prof Smith: Think of what happens when you dam a river. With a chronic obstruction, where there’s a collateral pathway, the pressure must show up as normal.
Dr Paul: So, the leading actor in vein hemodynamics is volume. To sum up: most procedures for treating varicose veins, including thermal ablation, phlebectomy, and so on, work because they reduce the volume.18
Prof Smith: Stockings as well. More exactly, they reduce the residual volume. The same is true for procedures aimed at correcting superficial19 and deep venous reflux.20,21.
Well, we just arrived at the Conference venue.
Dr Paul: Thanks for the chat. Now I know venous hemodynamics.
Prof Smith: Are you kidding? Venous hemodynamics is very complex,22,23 and I have only introduced some basic concepts. Many aspects of venous physiology and pathophysiology are not yet known, and others not yet studied. Only those who ignore the structural and functional complexity of this system can claim to have understood everything.
Dr Paul: I understand. I still want to thank you for introducing me to the problem without having to understand complex formulas.
Prof Smith: The complex formulas that you find applied to hemodynamics are often applied in an arbitrary way, as they are based on different experimental models. You will have the opportunity in the future to study all this, and you will probably be the one to master everything that I have not yet understood.
Conclusion
The complexity and partial knowledge of the hemodynamics of the venous system of the lower limbs makes it difficult to understand the mechanism of action of many therapeutic interventions, applied automatically by the phlebologist. A simple approach could pave the way to better understanding them, as well as encourage more complex studies. Those who find interest in this simple approach will be able to deepen their knowledge by reading the texts and the countless publications on this topic.

REFERENCES
1. Meissner MH, Moneta G, Burnand K, et al. The hemodynamics and diagnosis of venous disease. J Vasc Surg. 2007;46:4S-24S.
2. Shepherd JT. Role of the veins in the circulation. Circulation. 1966;33:484-491.
3. Arnoldi CC. Venous pressure in patients with valvular incompetence of the veins of the lower limbs. Acta Chir Scand. 1966;132:628-645.
4. Höjensgård IC, Stürup H. Static and dynamic pressures in superficial and deep veins of the lower extremity in man. Acta Phys Scand. 1952;27:49-67.
5. Pollack AA, Wood EH. Venous pressure in the saphenous vein at the ankle in men during exercise and change in position. J Appl Physiol. 1949;1:649-662.
6. Raju S. Use of air plethysmography and ambulatory venous pressure measurement in chronic venous disease. Phlebolymphology. 2020;27(2):52-60.
7. Neglen P, Raju S. Ambulatory venous pressure revisited. J Vasc Surg. 2000;31:1206-1213.
8. Nicolaides AN, Zukowski AJ. The value of dynamic venous pressure measurements. World J Surg. 1986;10:919-924.
9. Katz AI, Chen Y, Moreno AH. Flow through a collapsible tube: experimental analysis and mathematical model. Biophysical J. 1969;9:1261-1279.
10. Raju S, Fredericks R, Lishman P, Neglen P, Morano J. Observations on the calf venous pump mechanism: determinants of postexercise pressure. J Vasc Surg. 1993;17:459-469.
11. Lurie F, Kistner RL, Eklof B. The mechanism of venous valve closure in normal physiologic conditions. J Vasc Surg. 2002;35:713-717.
12. Qui Y, Quijano RC, Wang SK, Hwang NHC. Fluid dynamics of venous valve closure. Ann Biomed Eng. 1995;23:750- 759.
13. Lurie F, Kistner RL, Eklof B, Kessler D. Mechanism of venous valve closure and role of the valve in circulation. A new concept. J Vasc Surg. 2003;38:955-961.
14. Maleti O, Lugli M, Perrin M. Operative treatment in postthrombotic syndrome: an update. Phlebolymphology. 2014;21(3):131-137.
15. Nicolaides A, Maleti O. Lugli M, Guerzoni S. Noninvasive measurement of lower limb outflow resistance and implications for stenting. Vasc Invest Ther. 2019;2:88-94.
16. Kooijman M, Poelkens F, Rongen GA, Smits P, Hopman MTE. Leg blood flow measurements using venous occlusion plethysmography during head-up tilt. Clin Auton Res. 2007;17:106-111.
17. Nicolaides AN. Investigation of chronic venous insufficiency: a consensus statement. Circulation. 2000;102:e126-e163.
18. Christopoulos DG, Nicolaides AN, Szendro G, Irvine AT, Bull ML, Eastcott HH. Airplethysmography and the effect of elastic compression on venous hemodynamics of the leg. J Vasc Surg. 1987;5:148-159.
19. Nicolaides A, Kakkos S, Eklof B, et al. Management of chronic venous disorders of the lower limbs – guidelines according to scientific evidence. Int Angiol. 2014;33(2):87-208.
20. Maleti O, Perrin M. Reconstructive surgery for deep vein reflux in the lower limbs: techniques, results and indications. Eur J Vasc Endovasc Surg. 2011;41:837-848.
21. Maleti O, Lugli M, Tripathi R. Deep venous reconstructive surgery. Sem Vasc Surg. 2015;28(1):39-46.
22. Lee BB, Nicolaides AN, Myers K, et al. Venous hemodynamic changes in lower limb venous disease: the UIP consensus according to scientific evidence. Int Angiol. 2016;35(3):236-352.
23. Franceschi C, Zamboni P. Principles of venous hemodynamics. New York, NY: Nova Biomedical Books; 2009.